Leetcode
9 minutes read (About 1299 words) 0 visits

Leetcode 4. Median of Two Sorted Arrays

题目

4. Median of Two Sorted Arrays

  • Difficulty: Hard
  • Total Accepted: 301.7K
  • Total Submissions: 1.3M

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Exaple2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

题目链接

解题报告

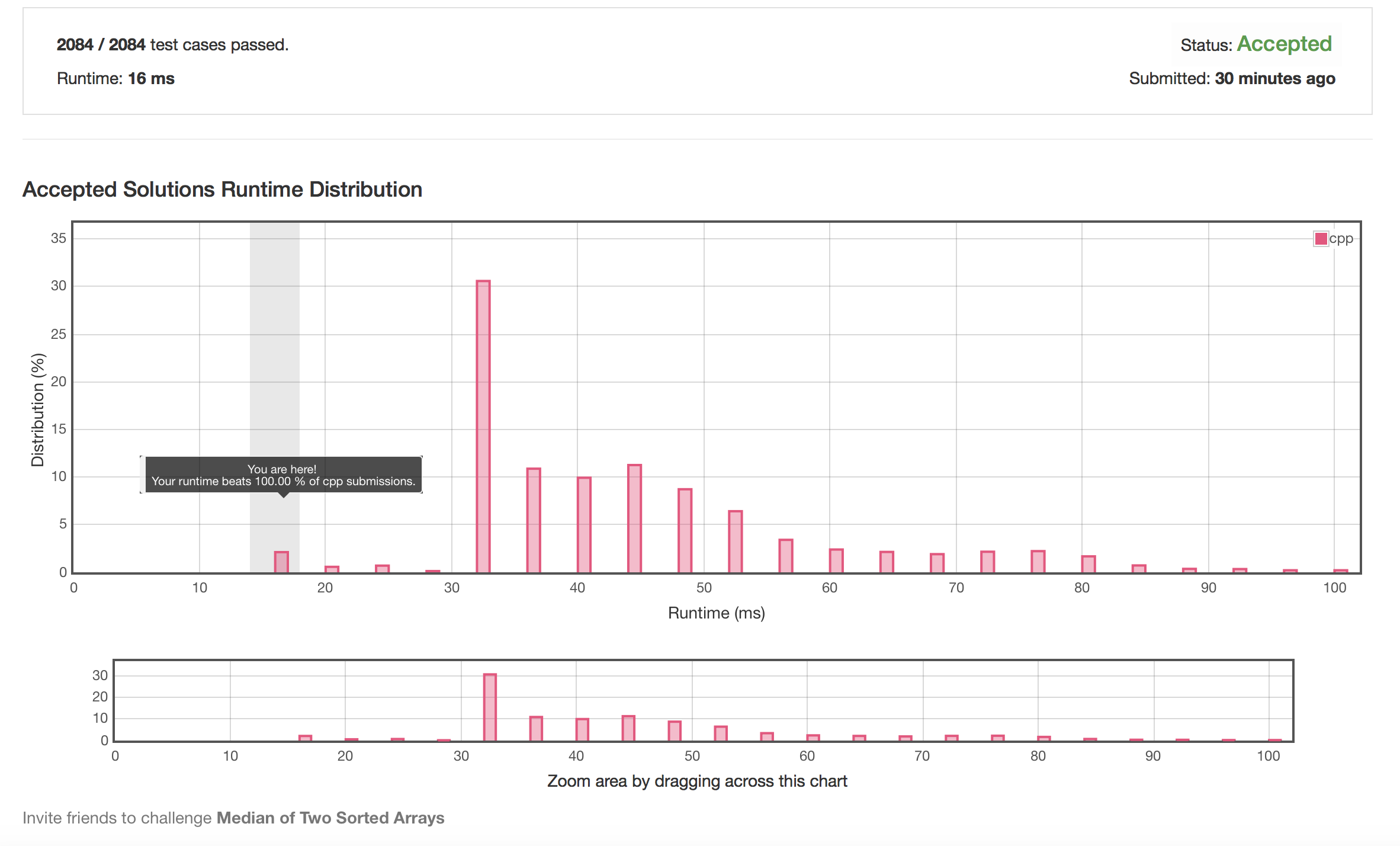
AC 截图

题目大意

本题要求寻找两个有序序列合并后的序列的「中位数」。同时要求 O(log (m+n)) 级别的时间复杂度。

解题思路

在一个序列中寻找一个数，又要求 O(log) 级的时间复杂度，我们很容易想到通过不断分割区间来寻找目标数的二分查找法。那么唯一的问题是如何在两个有序序列上应用针对单条序列的二分查找法了。

创建变量 start1、end1、start2、end2、halfSize，分别标识两个序列当前处理区间的头和尾，以及用于计数左侧较小数个数。通过不断对比两个区间中间数的大小，来使得中间数靠近，直到 halfSize 达到序列长度的一半即可（题解中为从一半减少到1）。

题解1

C++ 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {

public:
  
  double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int lengthSum = nums1.size() + nums2.size();

    return (lengthSum % 2 == 1) ?
      (double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), (lengthSum + 1) / 2):
      ((double)findMedian(nums1, nums2, 0, nums1.size(), 0,nums2.size(), lengthSum / 2 + 1) +
      (double)findMedian(nums1, nums2, 0, nums1.size(), 0,nums2.size(), lengthSum / 2)) / 2;
  }

  int findMedian(vector<int>& nums1, vector<int>& nums2, const int start1,
                const int end1, const int start2, const int end2,
                const int halfSize) {
    int size1 = end1 - start1, size2 = end2 - start2;

    if (size1 <= 0) return nums2[start2 + halfSize - 1];
    if (size2 <= 0) return nums1[start1 + halfSize - 1];
    if (halfSize == 1) return min(nums1[start1], nums2[start2]);

    int mid1 = (end1 + start1) / 2, mid2 = (end2 + start2) / 2;

    if (nums1[mid1] <= nums2[mid2]) {
      if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
        return findMedian(nums1, nums2, start1, end1, start2, mid2, halfSize);
      } else {
        return findMedian(nums1, nums2, mid1 + 1, end1, start2, end2,
                          halfSize - size1 / 2 - 1);
      }
    } else {
      if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
        return findMedian(nums1, nums2, start1, mid1, start2, end2, halfSize);
      } else {
        return findMedian(nums1, nums2, start1, end1, mid2 + 1, end2,
                          halfSize - size2 / 2 - 1);
      }
    }
  }

};

AC 截图

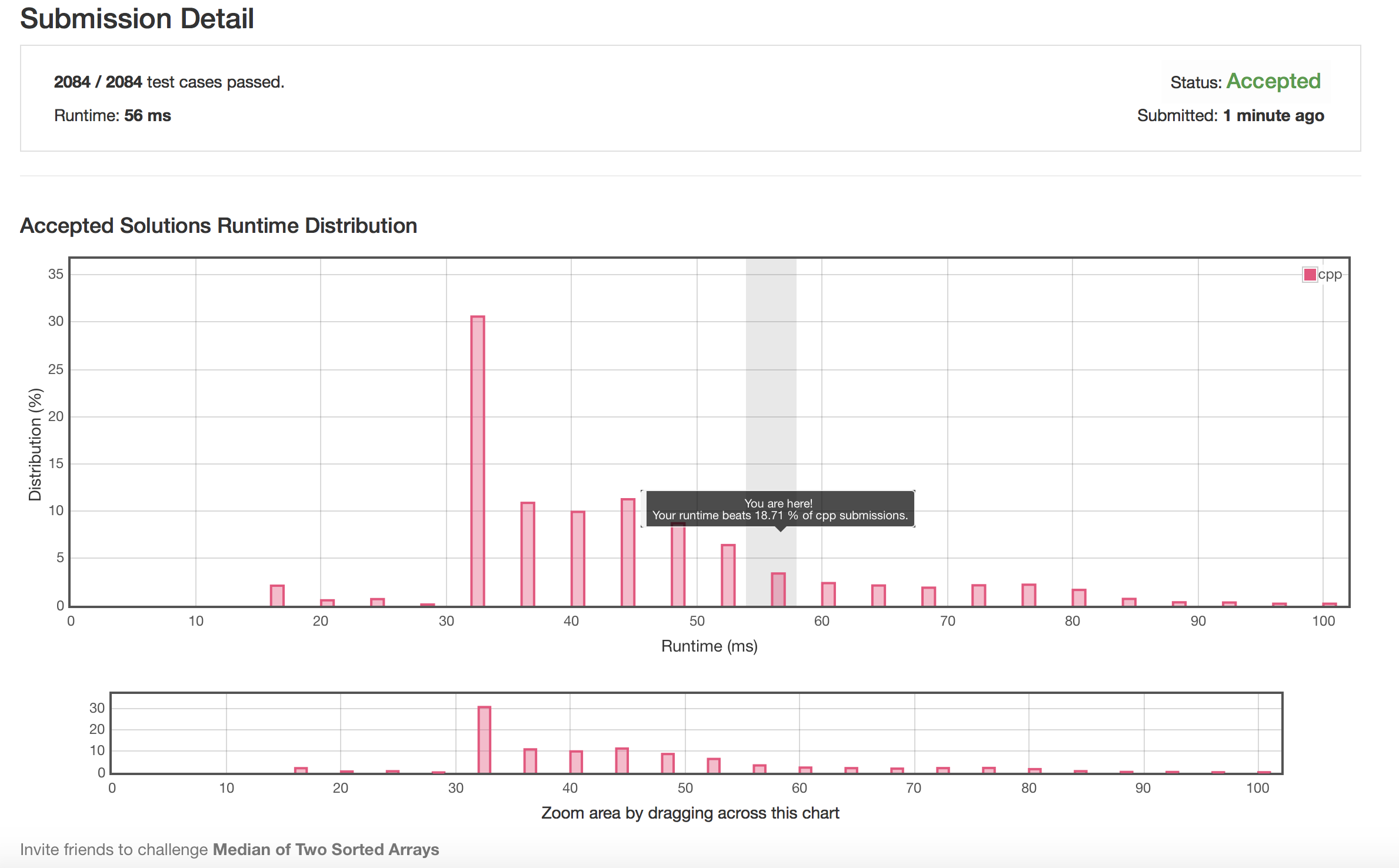
题解分析

虽然这个题解顺利通过了测试，但是我们发现，前面的最优解还有相当多……那么尝试对于代码进行优化。我们知道，递归方法相对于迭代法需要在每次递归时，对栈进行单独的操作——在空间和时间复杂度上都不如迭代法。

那么，是否可以把递归法转换为迭代法呢——当然可以啦～

题解2

C++ 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
 public:
  double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int lengthSum = nums1.size() + nums2.size();

    return (lengthSum % 2 == 1) ?
      (double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), (lengthSum + 1) / 2) : 
      ((double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), lengthSum / 2 + 1) +
      (double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), lengthSum / 2)) / 2;
  }

  int findMedian(vector<int>& nums1, vector<int>& nums2, int start1, int end1,
                 int start2, int end2, int halfSize) {
    int size1, size2, mid1, mid2;

    while (true) {
      size1 = end1 - start1;
      size2 = end2 - start2;

      if (size1 <= 0) return nums2[start2 + halfSize - 1];
      if (size2 <= 0) return nums1[start1 + halfSize - 1];
      if (halfSize == 1) return min(nums1[start1], nums2[start2]);

      mid1 = (end1 + start1) / 2;
      mid2 = (end2 + start2) / 2;

      if (nums1[mid1] <= nums2[mid2]) {
        if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
          end2 = mid2;
          continue;
        } else {
          start1 = mid1 + 1;
          halfSize -= size1 / 2 + 1;
          continue;
        }
      } else {
        if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
          end1 = mid1;
          continue;
        } else {
          start2 = mid2 + 1;
          halfSize -= size2 / 2 + 1;
          continue;
        }
      }
    }
  }
};

AC 截图

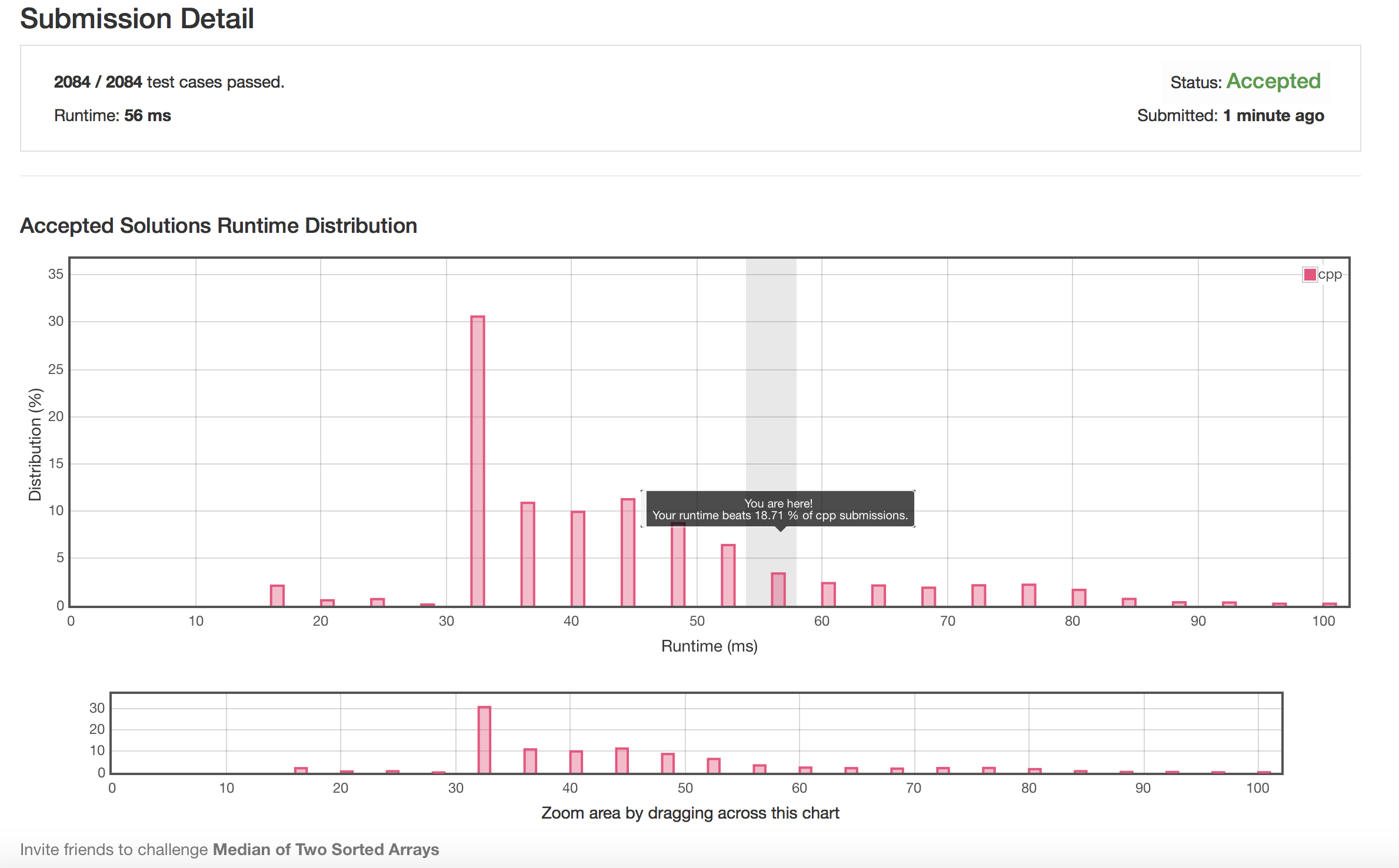
题解分析

嗯？这两个的耗时完全没有区别啊！看来是编译器已经把我的递归优化掉了……那么和第一梯队如此大的时间差又是从何而来呢？

参加过 ACM 的同学应该都知道，能用 scanf 的代码绝对不用 cin。不过其实 cin 的效率并不算差，只是，我们需要对其进行一些优化才能让他发挥出应有的实力。要想解放 cin 实力的封印，一行代码足矣：

ios::sync_with_stdio(false);

这会禁用 cin／cout 和 scanf／printf 之间的同步等待，从而大幅提升 cin 的效率——甚至可以直追 scanf。但是这里我们又有一个问题了，我们函数的调用显然是在输入操作之后，怎样才能让这个函数在输入操作前生效呢？当然是有办法的啦：

题解3（最优解）

C++ 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
static const auto runfirst = []() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    return nullptr;
}();

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
      int lengthSum = nums1.size() + nums2.size();

      return (lengthSum % 2 == 1) ?
        (double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), (lengthSum + 1) / 2) :
        ((double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), lengthSum / 2 + 1) +
        (double)findMedian(nums1, nums2, 0, nums1.size(), 0, nums2.size(), lengthSum / 2)) / 2;
    }

    int findMedian(vector<int>& nums1, vector<int>&nums2,
      int start1, int end1,
      int start2, int end2,
      int halfSize) {
        
        int size1, size2, mid1, mid2;
        
        while (true) {
            
            size1 = end1 - start1;
            size2 = end2 - start2;

            if (size1 <= 0) return nums2[start2 + halfSize - 1];
            if (size2 <= 0) return nums1[start1 + halfSize - 1];
            if (halfSize == 1) return min(nums1[start1], nums2[start2]);

            mid1 = (end1 + start1) / 2;
            mid2 = (end2 + start2) / 2;

            if (nums1[mid1] <= nums2[mid2]) {
              if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
                end2 = mid2;
                continue;
              }
              else {
                start1 = mid1 + 1;
                halfSize -= size1 / 2 + 1;
                continue;
              }
            }
            else {

              if (size1 / 2 + size2 / 2 + 1 >= halfSize) {
                end1 = mid1;
                continue;
              }
              else {
                start2 = mid2 + 1;
                halfSize -= size2 / 2 + 1;
                continue;
              }
            }
      }
    }
};

AC 截图

题解分析

通过声明一个静态的常量变量，我们使得后面这个自执行的函数甚至可以在编译阶段预执行，从而在输入输出前完成对于 cin/cout 的设置～总时耗也从 56ms 下降到了 16ms，妥妥的第一梯队～看来算法和实现细节都是保证程序执行速度的重要环节呢。

# Algorithm, Leetcode
Leetcode 124. Binary Tree Maximum Path Sum
Service Computing 01 - Private Cloud Service
Follow

Links

Categories

Tag Cloud

Algorithm Assignment Blockchain Cloud Service Decision Tree Ensemble Learning Ethereum Github Pages Gitment Golang JavaScript Leetcode Machine Learning OpenAPI RESTful Remote Floder SSAD Service Computing Unity3D VPS server WEB Windows

Recent

Archives

Tags

Algorithm 15
Assignment 5
Blockchain 1
Cloud Service 2
Decision Tree 3
Ensemble Learning 3
Ethereum 1
Github Pages 1
Gitment 1
Golang 2
JavaScript 3
Leetcode 14
Machine Learning 3
OpenAPI 1
RESTful 1
Remote Floder 1
SSAD 7
Service Computing 4
Unity3D 9
VPS server 1
WEB 6
Windows 1

Recent

Archives

Tags

Algorithm 15
Assignment 5
Blockchain 1
Cloud Service 2
Decision Tree 3
Ensemble Learning 3
Ethereum 1
Github Pages 1
Gitment 1
Golang 2
JavaScript 3
Leetcode 14
Machine Learning 3
OpenAPI 1
RESTful 1
Remote Floder 1
SSAD 7
Service Computing 4
Unity3D 9
VPS server 1
WEB 6
Windows 1
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×